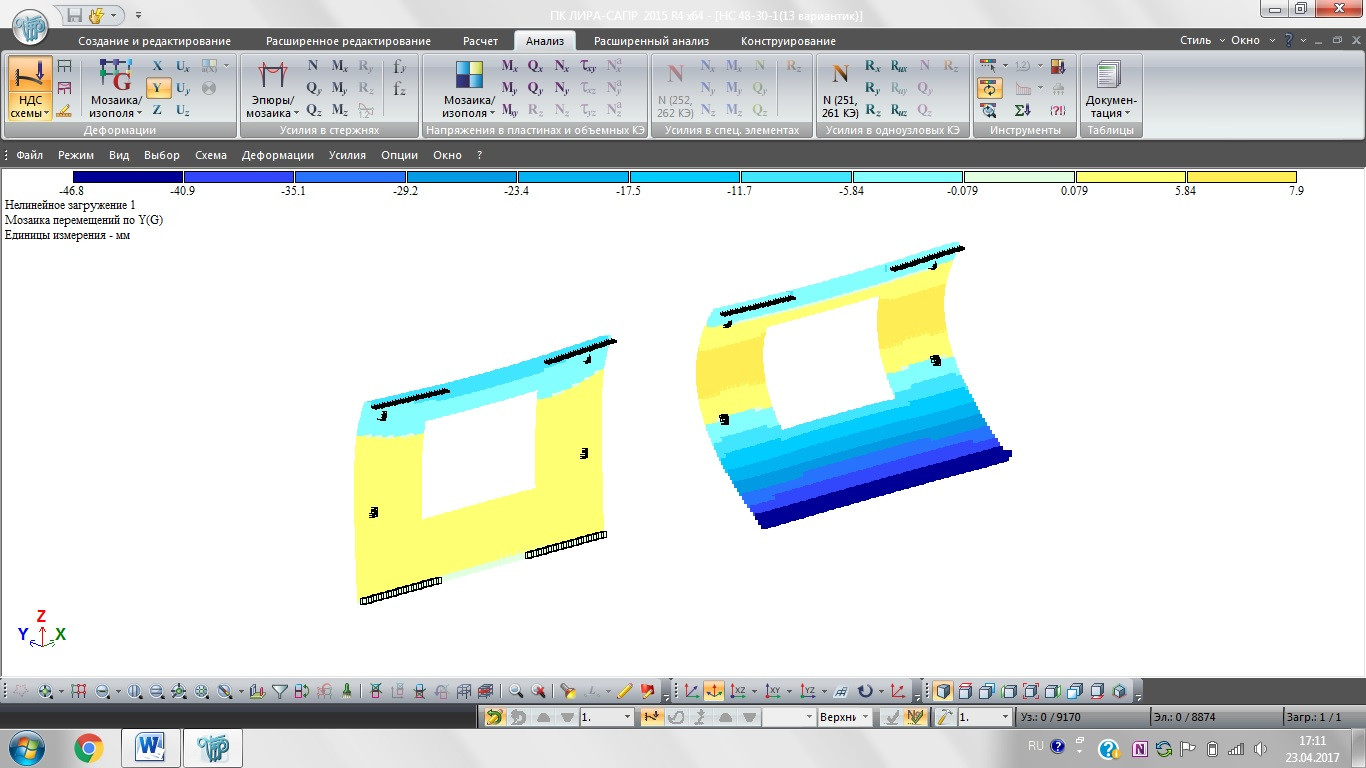
Смещение стеновой панели при расчётной нагрузке

Рубрика #вопрос-ответ

Моделируем стеновую ж/б панель. Возникает вопрос с закреплением.

Слева на картинке панель замоделирована с жестокстями растворного шва, т. е. как-то закреплена по всем 6-ти направлениям.

Справа панели закреплена по оси «Z» и от поворотов (всех 3-х), сделала там, потому что эту панель испытали отдельно одну и никаких закреплений кроме этих на схеме испытаний не показано.

Низ левой панели почти не двигается, это вроде хорошо. Низ правой панели «уехал» и по Х и по Y (1–5 см).

По деформациям по оси Y обе панели работают корректно (судя по результатам испытаний), но правая все-таки ближе.

Вопрос, могу ли я допустить в расчетной схеме, что плита толщиной 200 мм при расчетной нагрузке 100% может уехать на 50 мм?

Отвечает Шатров Евгений Юрьевич Автор и ведущий курсов «ЛИРА-САПР», эксперт в области прочностного анализа, квалифицированный инструктор ПК «ЛИРА-САПР», экс-доцент кафедры «Строительная механика» Южно-Уральского государственного университета,

Стандартная модель (в ПК «ЛИРА-САПР») строится (среди прочего) в рамках гипотезы малых деформаций и перемещений.

Для панели толщиной 200 мм смещение в 50 мм составляет четверть толщины. Это больше, чем пятая часть, что является критерием для вышеназванной гипотезы (см. учебник В. А. Икрина Сопротивление материалов…, раздел «Основы технической теории тонких жёстких пластинок», самое начало раздела). Таким образом, для вашей модели эта фундаментальная предпосылка, в рамках которой отыскивается решение, нарушается. Значит, оно (решение) не является корректным.

В данной ситуации мы учитываем, что в физическом смысле ваша модель линейно упруга.